MATEMATICAS I

matematicas I

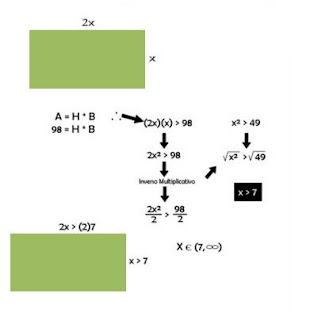
Si un jardin rectangular tiene su longitud el doble de su ancho Si el area encerrada debe ser mayor que 98m² ¿que puede decir el ancho del jardin?

inecuaciones

En las demas inecuaciones son solo el resultado

La siguiente inecuacion es :

respuesta

Esta es una igualdad

respuesta

numeros racionales finitos

Tambien conocidos como numeros racionales ilimitados son los que en su presentacion decimal tienen un numero fijo de numeros.

Ejemplo:

numeroes racionales periodicos

Estos numeros son los que en su presentacion decimal tienen un numero ilimitado de numeros.

Hay dos tipos de numeros racionales periodicos: Los periodicos puros: Un numero, o grupo de numeros, se repite ilimitadamente a partir del segundo o posterior deimal, ejemplo:











Y los periodicos Mixtos: un numero o grupo de numeros se repite ilimitadamente a partir del segundo o posterior decimal por ejemplo (3.27838383838383)

Axioma de orden

Se dice que los axiomas de orden establecen una relacion o cantidad. Es decir que no son igualdades y que ciertos valores tienden a ser menores que, mayores que, menor o igual que, mayor o igual que,...Estas propiedades se representan con los simbolos:

<: Menor que...

>: Mayor que...

: Menor o igual que...

: Mayor o igual que...

En una relacion de numeros se debe mantener orden en donde es nesesario utilizar el simbolo <>Existe un subconjunto R⁺ de R tal que:

i) Si a, b ÎR⁺, entonces a + b ÎR⁺

a . b ÎR⁺

Para cada a ÎR , una y solo una de las siguientes proposiciones es verdadera.

a ÎR⁺ ; a = 0 ; -a ÎR⁺.

Los elementos a ÎR , para los cuales a ÎR⁺, serán llamados: reales positivos.

Los elementos a ÎR , para los cuales -a ÎR⁺, serán llamados: reales negativos.

Desigualdades

Usando solamente el subconjunto R⁺ descrito en A.O.1., se deducen todas las reglas usuales en el trabajo con desigualdades de números reales.

Cada una de las expresiones: x <> y, x y, x y es llamada una desigualdad.

Se sigue de la definición anterior que las desigualdades: x > y, y, y < src="http://huitoto.udea.edu.co/Matematicas/imagenes/Mayorigual.gif" height="20" width="16"> y, y, y x son equivalentes.

La expresión: x <> y > z, se usa para indicar las dos desigualdades simultáneas: x > y ^ y > z.

En cualquiera de los dos casos de la definición anterior, se dice que y está entre x y z.

Propiedades de los exponentes

El exponente o potencia es un elemento que multiplica al factor por si mismo dependiendo del valor del elemento en este caso se llama exponente.

Ejemplo:

aⁿ = (a)(a)(a) . . .(a) n veces

Los exponentes indican que un número se esta multiplicando por si mismo n veces.

Es decir que sube de valor duplicandose a si mismo

Ejemplo:

= 10 * 10 * 10 = 30

Un número puede descomponerse en n factores deseados

a⁰ = 1

a¹ = a

a² = (a)(a)

a³ = (a)(a)² = (a)(a)(a)

a⁴ = (a)(a)³ = (a)(a)(a)(a)

aⁿ = (a)(a)^n-1 = (a)(a)…(a) n factores del mismo dependiendo del valor de n

Nota: toda base elevada a la 0 potencia es igual a 1

Primera ley: Producto de potencias con la misma base.

Ejemplo:

a³ • a²

Por la definición de potencia se tiene:

donde a aparece 5 veces como factor, por lo tanto:

a³ • a² = a³+²

=

Esto significa que en la multiplicacion los exponentes que tienen la misma base se suman

Segunda ley: Cociente de potencias con la misma base

Ejemplo:

Por la definición de potencia se tiene que:

Al cancelar factores iguales quedaria:

En conclusion con la segunda ley deduci que en la divicion de exponentes con la misma base los exponentes se restan de manera eliminativa.

Tercera ley: Potencia de una potencia

Ejemplo:

Por la definición de potencia se tiene:

Apoyándose en la ley 1;

Entonces se dice que el exponente de un exponente de la base es igual a la base elevada al producto de los exponentes

Cuarta ley: Potencia de un producto

Ejemplo: (ab)³

Al aplicar la definición de potenciaen este caso seria:

(ab)³ = ab • ab • ab

Aplicando la ley conmutativaquedaria de la siguiente manera:

(ab)³ = a * a * a * b * b * b

Y como la potencia es una multiplicación abreviada, queda:

a³b³

Entonces quedamos en que la potencia de un producto es igual al producto de la potencia an ambos factores del producto es decir, es igual que el producto de la misma potencia de los factores

Quinta ley: Cuando un cociente se eleva a una potencia

Ejemplo:

Aplicando la definición de potencia quedaria de la siguiente manera:

Abreviando la multiplicación de fracciones se simplifica quedando asi:

Esto quere dar a entender que si se eleva una fraccion a un exponente n se eleva el numerador y el denominador de dicha fraccion

en otros casos de fracciones cuando se tiene un exponente como fraccion elevado a otra potencia seria lo siguiente




Entonses quedaria:




aplicando la primera ley quedaria el resultado de la siguiente manera:

Axioma de Campo
Un axioma es lo logico o evidente para despues deducir o predecir la conclucion de la resolucion de problemas con numeros reales Existen seis axiomas de campo de los numeros naturales

Axioma de campo 1: Asociativa
Se dise que si dos numeros estan asociados en una suma de producto de tres numeros, es independiente, es decir que la manera en que se agrupan es de manera singular independiente

( a + b ) + c = a + ( b + c ) y ( a * b ) c = a ( b * c )

Axioma de campo 2: Conmutativa
En la ley conmutativa nos dice en pocas palabras que el orden de los factores no altera el producto, es decir que el producto no es dependiente de la forma del orden de los factores comunes de la operacion

a + b = b + a y a * b = b * a

Axioma de campo 3: Distributiva
La ley distributiva tambien llamada ley del mosquetero nos explica que si tenemos un termino que se multiplica com otros dos ya asosiados, este se debe operar reciprocramente, es decir por cada uno de los terminos asosiados.

a ( b + c ) = ab + ac

Axioma de campo 4: Identidad
Esta les no es mas que los elementos de identidad es decir con que se identifica una incognita

Para cualquier existe un real llamado “cero” denotado por 0 tal que Para cualquier existe un real llamado “uno” denotado por 1 tal que Existencia del neutro Existe un número, el cero 0, tal que, a + 0 = a Existe un real ≠ 0 , el número 1, tal que a ⋅ 1 = a Para cada real a existe su inverso aditivo, con existencia de inversos que denotaremos con (− a) tal que a +(− a)= 0